TextilePlot
変量が多い,つまり高次元空間上の点の集まりとして表される大量記録でも,まずはデータそのものの姿を眺めることが重要です.TextilePlotはそれを助ける強力な視覚化ソフトウエアです. 高次元空間の座標軸を縦に並べ, 座標を結んだ一つの折れ線で一つの記録を表す「並行座標プロット」の一種で,各折れ線がなるべく水平に近くなるように,各座標軸の尺度と位置を定める以外,何らの加工もしていないことが特徴です.つまり,数値や文字で表されたデータをそのものを眺める代わりに,その様子を視覚的に把握できる道具です. また,この「水平性基準」により,各カテゴリカル変量の水準の位置も定まりますので,数値データにカテゴリカルなデータが混在しても,欠損値が存在しても構わないオールラウンドな視覚表現です.TextilePlot がどんなものか少しでも理解していただくため,以下にごく簡単な例をいくつか掲げます.現在では,TextilePlotは,独立したDandDクライエントソフトウエアではなく, TRAD の基本的なヒューマンインターフェースとなっておりますので,TRADをダウンロードしてお試しください.
例 Iris Data
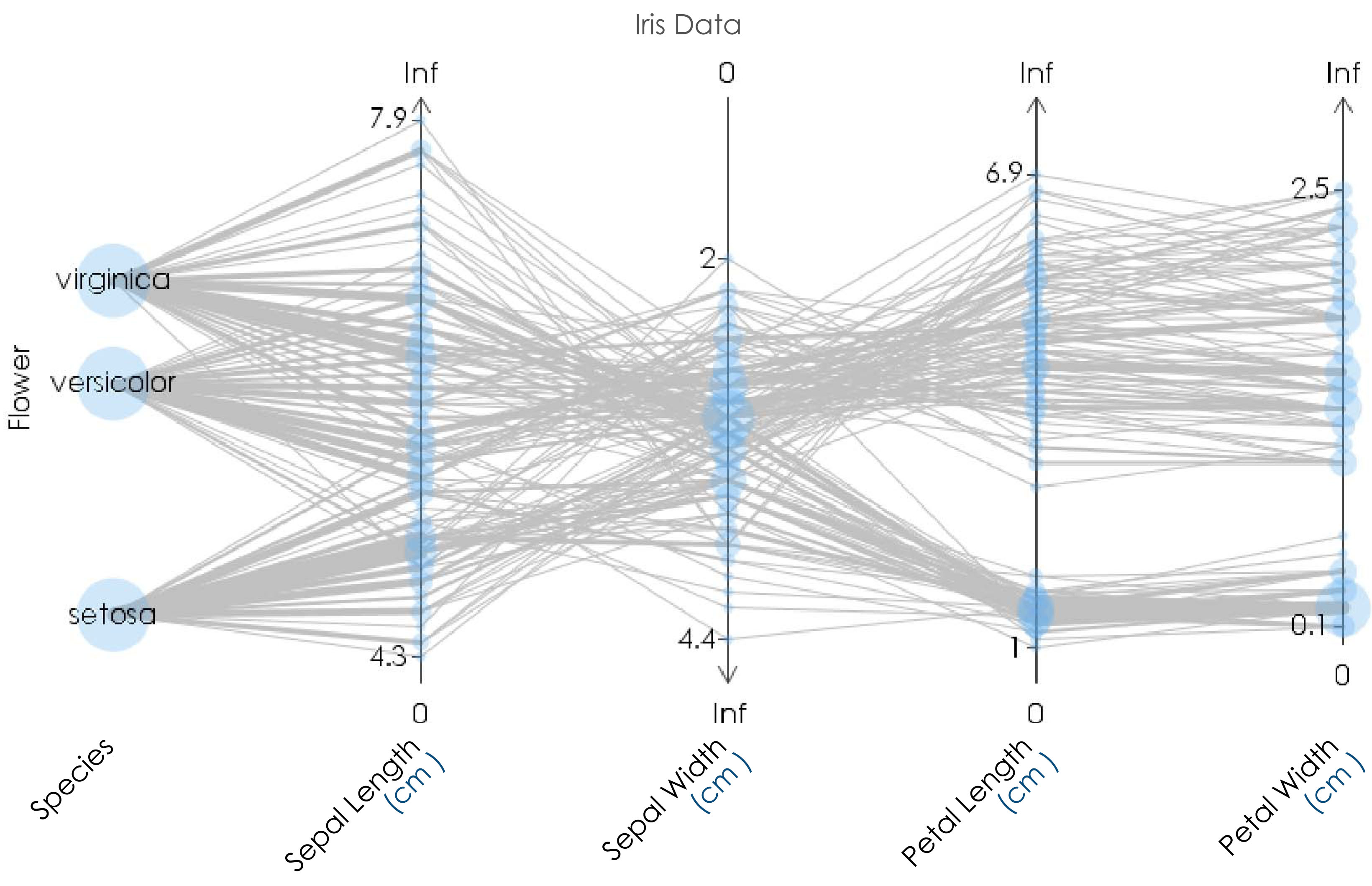
古くからデータ例として頻繁に用いられてきたアヤメデータのTextilePlotです.3種(species)のアヤメの花の花弁(petal)の長さと幅,萼片(sepal)の長さと幅の記録150件が表示されています.したがって,折れ線は150本あり,それぞれの折れ線一本が記録一つを表しています.それぞれの記録が「何の値の組か」であるかを示すため, TextilePlot の左端には記録の対象が示されています.この場合は Flower で,アヤメの花が記録の対象であることを示しています.
アヤメの種類(Virginica, Versicolor, Setosa) はカテゴリカル な変量 Species で表されていますが,その座標は「水平性基準」 により定まっています.ただ,その座標そのものに特に意味はありませんので 座標軸は描かれていません.言い換えれば,TextilePlotで座標軸が引かれていない 変量はカテゴリカルな値をとる変量であることになります.種Virginica, Versicolor, Setosa それぞれが円板で表されていますが,その直径は 記録数に比例しています.この場合には,それぞれの種類について50件,記録されています ので,当然同じ直径の円板で表されています.
残りの変量はすべて数値変量ですので座標軸が引かれています.上下にある数値は 可能な値の範囲を表しています.この場合,0 と Inf(無限大)になっていますので, 正の値しかとらないことを表しています.幅や長さですから当然です.実際にデータ として現れた値の最大値と最小値は座標軸上の目盛であらされています.たとえば Sepal Length (顎の長さ)の最大値は7.9, 最小値は4.3であることがわかります.また,小さな円板が描かれている箇所もありますが,これは重複した値であることを表しています. カテゴリカルの場合と同じように,円板の直径は重複数に比例します.このアヤメの データは,0.1 cm 単位で記録されていますので,当然このような重複値が存在します. 数値だけを眺めていると見過ごすようなこのような特徴もTextilePlotなら即座に理解できます. 一つ,注意していただきたいのは,Sepal Width(愕の幅)の軸の向きが逆転している点です. これは,「水平線基準」からすると,この変量だけは他と逆の動きを示していることがわかります.各軸名にかっこ書きされているのは単位です.この場合いずれも cm であることがわかります.
TextilePlot は当然,座標軸を並べる順序によって異なる印象を与えます. 上の図は,ディフォルトの場合で,もとのデータファイルでの出現順をそのまま反映して います.もともと自然な順序で並んでいれば,この ディフォルトのままでよいのですが,そうでない場合は,並べる順序の工夫が 必要です. その一つの答えが「座標軸のクラスタリング」です.2つの座標軸の 間の「距離」を,その間を結ぶ線分の水平からの乖離として定義すれば,階層的な 座標軸のクラスタリングが行えます.その結果を反映するように座標軸を並べ替えた TextilePlot が次の図です.
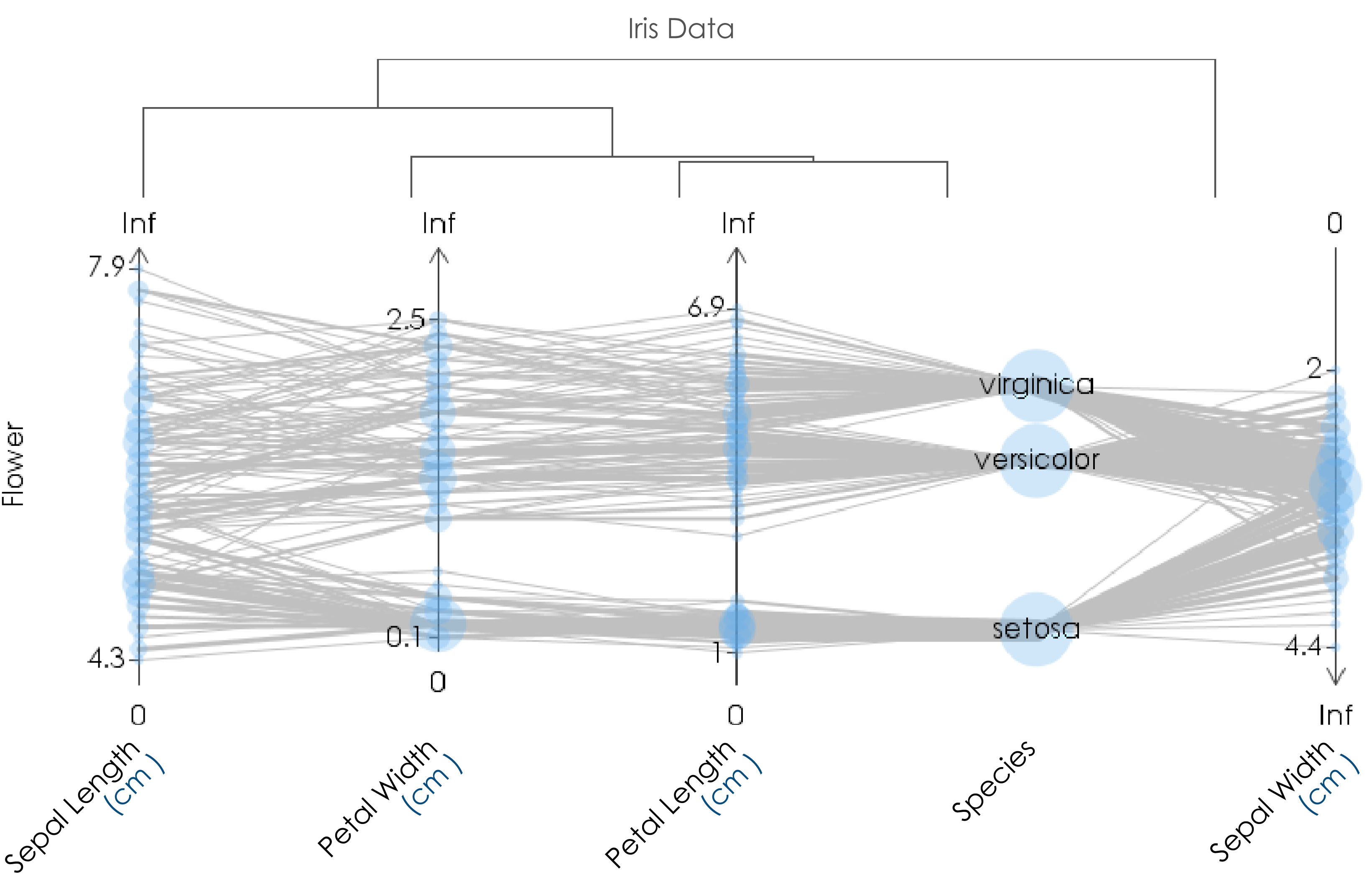
上部に描かれた「木」が座標軸の階層的なクラスタリングを表しています. このTextilePlot を眺めると,このデータの様子は一目瞭然でしょう. Species (種)にもっとも近い変量は Petal Length (花弁の長さ)であり, 種 Setosa は,この花弁の長さだけで100% 他の種と区別できることが わかります.次に近い変量は Petal Width (花弁の幅)ですが,Petal Length とかなり水平に近い線分で結ばれているので,種の区別には補助的にしか 役立たないだろうということが推測されます.結局,残りの種, Virginica, Versicolor の区別をするとしたら,花弁が長い種を Virginica, 短い種を Versicolor と判断し,補助的に花弁の幅を用いることになるだろうという直感が得られます.
このアイリスデータは,これまで判別分析やサポートベクターマシンのテストデータとしてよく利用されてきたのですが,TextilePlot でデータそのものを視覚的に眺めるだけで,このような高級な道具を持ち出すまでもなく,同じことがきわめて直感的に理解できることがわかります.さらに,各変量ごとの値の分布状態や,どのような記録が多いかなど,興味に応じてさまざまな観点から データを吟味できます.たとえば,はずれ値があるかないかなども重要な要素ですが,高級な道具を使うと見えなくなってしまうような少数のはずれ値などもいくらでも詳細に調べられることになります.実際には,TextilePlot のさまざまな機能を利用して,注目したい条件での記録をのこしたり,変量を落としたり,モデルの探索を進めるとになります.
例 Kyphosis Data
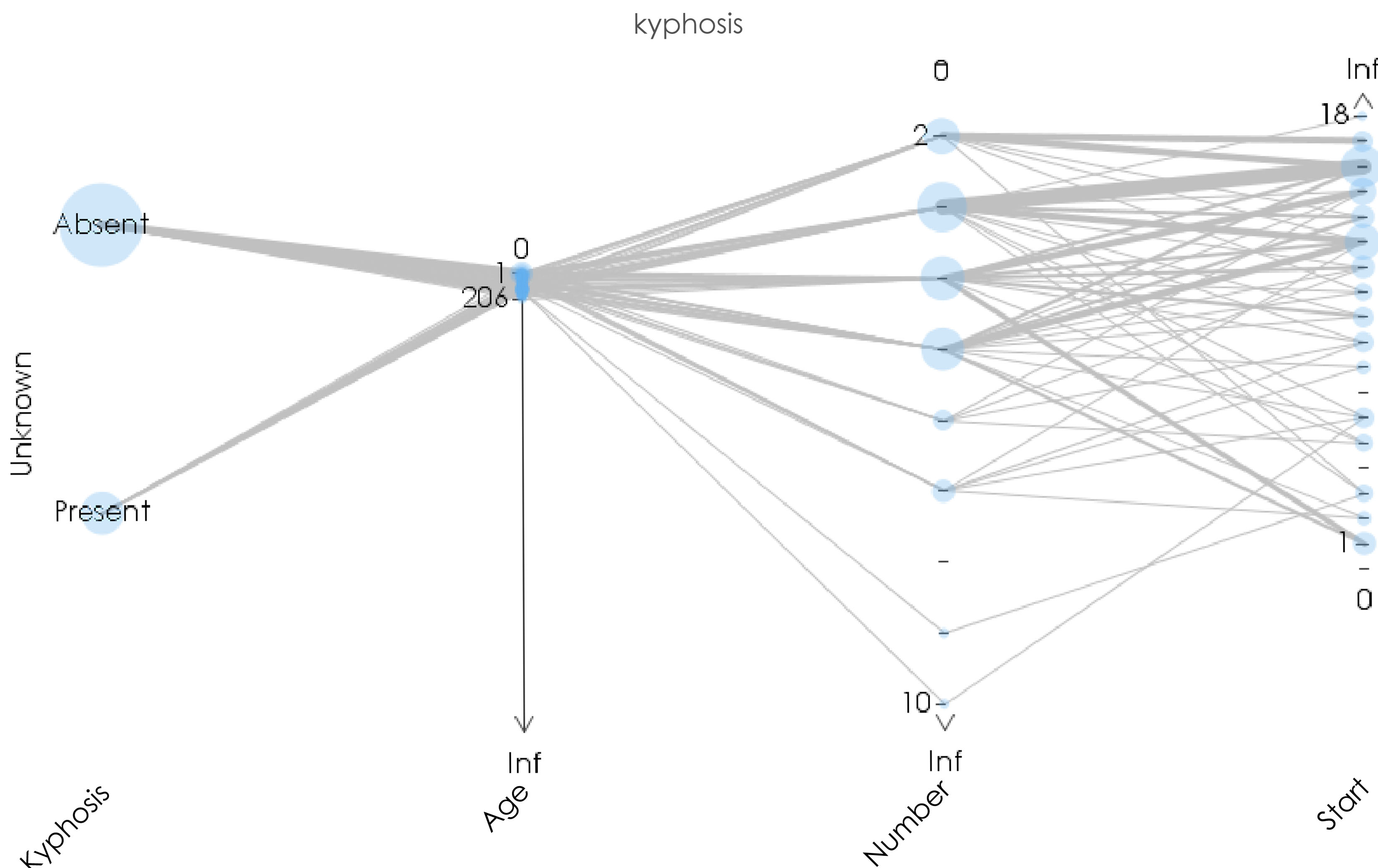
このデータも,よく例として用いられることの多いデータで,子供の脊椎湾曲症(Kyphosis) が手術で治るかどうかの記録81件からなるデータです.CSV ファイルをTextilePlot にドラッグして簡易に描いたTextilePlot なので,記録の対象はChild(子供)にも関わらず,Unknown となっており,単位も記入されていません.各軸の名前は,CSVファイルの第一行を参照して定められています.もっとも左の座標軸は,2 水準 Absent と Present を持つカテゴリカル変量 Kyphosisに対応する軸で,Absent が手術後も脊椎湾曲が直った, Present が直らなかったことを示しています.円板の大きさをみれば,直ったケースのほうが 多いものの,直らなかったケースもそれなりに存在することがわかります.その隣の座標軸は 手術時の生後月数を示す変量 Age に対応する軸で,最大 206 か月の患者までいたことが わかります.しかし,この軸の尺度は極めて大きくとられており,座標がかなり固まって 配置されています.TextilePlot でこのようなノット(knot, 節)が生まれるのは,その変量が他の変量と直交しているときであることが分かっています.したがってこの場合,手術の成否は 生後月数とほとんど関係ないことがすぐわかります.
残りの2つの座標軸は,手術した椎骨の個数を表す変量 Number と,手術開始位置を 表す椎骨の番号 Start に対応する軸です.ここで,これらの座標軸の表現の仕方が カテゴリカルの場合とも,数値の場合とも違うことに注意していただきたい.カテゴリカル の場合に似てはいるものの,下向きあるいは上向きの矢頭がそれぞれの軸に置かれている. つまり,これは水準に順序のある順序カテゴリ変量の表示となっている.さて,アイリス データのときと同じように,座標軸の階層的クラスタリングで軸の順序を定めたらどのようにみえてくるでしょうか.
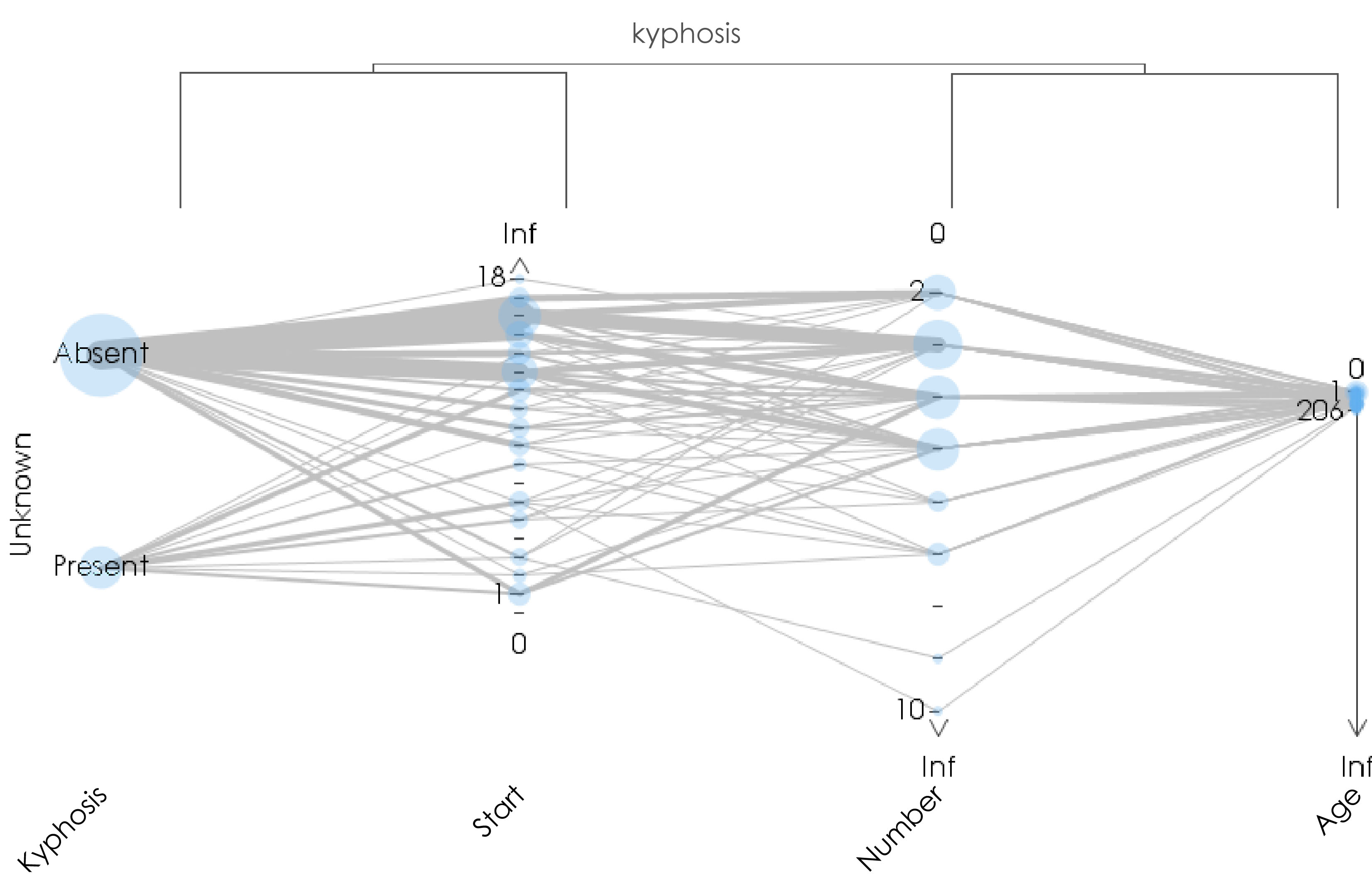
このTextilePlotはすでにある程度の答えを出しています.つまり手術の成否を決める 第一の要因はStartで,手術開始位置が大きく,つまり頭から離れた位置であれば 成功する可能性が高まることを示唆しています.Number も手術の成否にある程度の 関係があり,手術する椎骨の個数が多くなれば成功率が下がることは,軸の方向が Startとは逆であることからも見てとれるとおもいます.さらにクラスタ木をみると, Number と Age の間にもなんらかの関係はありそうなことがわかります.これは 手術の成否とは直接関係なく,生後月数が多くなればなるほど手術する必要のある椎骨の数も増えるという,患者の状態を示しているにすぎないのかもしれません. いずれにしろ,これから先は GLM(Generalized Linear Model) などよく知られた モデリング手法をいろいろ試して,より説明力のあるモデルを探索していくことになります.しかし,TextilePlot で養ったこのデータに関する基本的な認識は,そのモデル探索の段階で必ず大きな役割を果たすに違いありません.
